vehicle routing problem

The Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) is a combinatorial optimization problem that aims to find the optimal set of routes for visiting a set of locations, using a fleet of homogeneous vehicles. The problem’s objective is to minimize the total traveling distance, while satisfying vehicle capacity and service time window constraints.

Over the last 60 years, the CVRPTW has continuously attracted attention from both Operations Research and Computer Science research communities. Solving the CVRPTW can significantly improve operational costs, alleviate last-mile delivery burden, mitigate environmental impact, and enhance customer satisfaction. However, this is a challenging task, as the size of the solution space grows exponentially with the size of the problem.

In this project, I revisited the classic CVRPTW and attempted to develop a high-quality solution method. The slides below summarized my work including description of the research problem, related works, a BnP solution method by column generaton approach, solution development, result analysis, conclusion and directions for future research.

In the following sections, I will explain different mathematial formulations of the presented routing problem. A conventional MILP model will be described first and serve as foundation for applying DWD and reformulating a new model. Understanding this problem modeling is core to understand how a BnP solution method using column generation works.

MILP Model

Let define the CVRPTW on a network \(G\), which is constructed from a set of vertices \(V\) and a set of edges \(E\). The network graph is then modeled as \(G = (V,E)\). Consider the set of vertices \(V\), it includes a central depot and all customers. Thus, \(V = 0,1,2,...,n\), where vertex \(0\) represents the central depot and \(n\) remaining vertices represent customers. Consider the set of edges \(E\), it includes all pair of different vertices. Thus, \(E = \{(i,j) \mid i, j \in V,\ i \neq j\}\). Each edge \((i,j)\) belonging to \(E\) is associated with a traveling cost \(c_{ij}\) (equivalently, traveling time and distance). In regards of vehicles, there is a fleet of homogeneous vehicles \(K\) with carrying capacity \(Q\). Given \(K = 1,2,...,\|K\|\), each vehicle \(k \in K\) is assigned a delivery route, starting and ending at the central depot. A vehicle must not leave the depot before its earliest time \(a_0\) and must not return to the depot after the latest time \(b_0\). Next, in regards of delivery requests, each request is associated with a location \(i \in V{\setminus}\{0\}\), a service time \(s_i\), and a time window \([a_i,b_i)\). It is critical that customer time windows are respected, meaning vehicles must arrive at customers during their active time interval. Finally, the problem objective is to find a minimum-cost set of routes that visit each customer exactly once while not violating capacity and time window constraints.

\[\text{Min} \sum_{k \in K}\sum_{(i,j) \in E}c_{ij}x_{ij}^k \tag{1}\] \[\text{S.t.} \sum_{k \in K}\sum_{\{j \in V \mid (i,j) \in E\}}x_{ij}^k \quad \forall i \in V{\setminus}\{0\} \tag{2}\] \[\sum_{\{j \in V \mid (i,j) \in E\}}x_{ij}^k \quad - \sum_{j \in V \mid (i,j) \in E\}}x_{ji}^k = 0 \quad \forall i \in V, \forall k \in K \tag{3}\] \[\sum_{\{j \in V \mid (0,j) \in E \}}x_{0j}^k \leq 1 \quad \forall k \in K \tag{4}\] \[\sum_{\{i \in V \mid (i,0) \in E\}}x_{i0}^k \quad - \sum_{\{j \in V \mid (0,j) \in E\}}x_{0j}^k = 0 \quad \forall k \in K \tag{5}\] \[\sum_{(i,j) \in E}q_{i}x_{ij}^k \leq Q \quad \forall k \in K \tag{6}\] \[w_i^k + s_i^k + t_{ij} \leq w_j^k + M(1 - x_{ij}^k) \quad \forall (i,j) \in E, j \neq 0, \forall k \in K \tag{7}\] \[w_i^k + s_i^k + t_{i0} \leq b_0 + M(1 - x_{ij}^k) \quad \forall (i,0) \in E, \forall k \in K \tag{8}\] \[a_i \leq w_i^k \leq b_i \quad \forall i \in V, \forall k \in K \tag{9}\] \[x_{ij}^k = \{0,1\} \quad \forall (i,j) \in E, \forall k \in K \tag{10}\]

The above model solves for two decision variables \(x_{ijk}\) and \(w_{ik}\). The first decision variable, \(x_{ijk}\), is binary variable. \(x_{ijk} = 1\) if vehicle \(k\) travels edge \((i,j)\), \(x_{ijk} = 0\) otherwise. The second decision variable, \(w_{ik}\), states the starting time of service by vehicle \(k\) at customer \(i\).

Objective function \((1)\) aims to minimize the overall traveling cost (equivalently, traveling time and distance) within system. Constraint \((2)\) is covering constraint, stating that each customer is visited exactly once. Constraint \((3)\) is flow conservation constraint. It ensures the total number of arcs entering a node is equal to the total number of arcs leaving that node. Constraint \((4) - (5)\) are route-construction constraints, enforcing each vehicle to start and end their delivery journey at the depot. The next constraint, \((6)\), is capacity constraint. A vehicle cannot carry more than its capacity. Another resource constraint is time constraint. Constraints \((7) - (9)\) declare that delivery service must respect customer and depot time window. In addition, constraints \((7) - (8)\) also assure subtour eliminations. Constraint \((10)\) is binary constraint for decision variable \(x_{ijk}\).

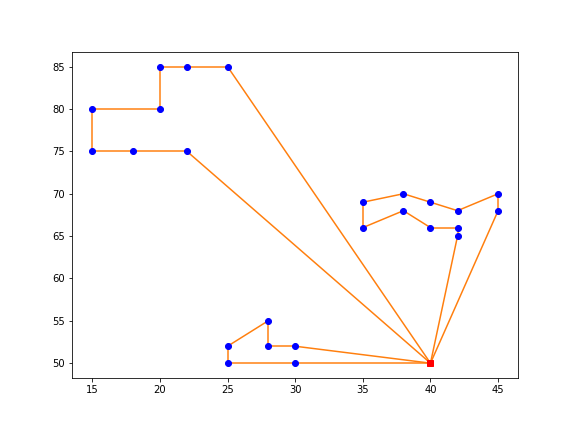
The MILP model above can be solved directly by commercial solvers for small-size instances, usually less than or equal to 25 customers. The figure below displays a plot of final routes obtained by GUROBI solver for Solomon problem C101 with 25 customers. Find the code here.

Reformulated Model by Dantzig-Wolfe Decomposition

Structure and Dantzig-Wolfe decomposition

The linear relaxation of the MILP model described in the previous subsection is very weak. As the number of nodes increases, the number of binary variables also increases significantly. Relaxing too many binary variables improves computational burden but eventually diminishes the effectiveness of BnB solution method. This limitation is the motivation for study of another reformulated version of the model.

Looking closely at the structure of the MILP model, it is revealed that only constraint \((2)\) in the model is grouping vehicles, meanwhile all other constraints are examining each vehicle separately. Moreover, it is assumed that vehicles are identical. This property implies that decomposition methods can be applied to break a master problem, which basically deals with constraint \((2)\), into \(\|K\|\) subproblems, which basically deals with the rest of constraints. LR and DWD are the most widely studied methods for decomposition of the CVRPTW. Both decomposition schemes alternate between solving the master problem and subproblems. DWD method does so using the help of dual variables. Meanwhile, LR method makes use of Lagrangian multipliers. Desrosiers et al. (1995) demonstrated that DWD method is superior to LR method in terms of both time complexity as well as solution quality.

Master Problem

The column generation approach exploits DWD to attain a reformulated version with better linear relaxation. Let \(R^k\) be the set of feasible routes for vehicle \(k\), \(k \in K\). Then \(r \in R^k\) corresponds to an elementary route traversed by $k$. Let \(x^{k}_{ijr}\) be a binary variable, where \(x^{k}_{ijr} = 1\) if \((i,j)\) is on route \(r\) and \((i,j)\) is traversed by \(k\), \(x^{k}_{ijr} = 0\) otherwise. Let \(y^{k}_{r}\) be a binary variable, where \(y^{k}_{r} = 1\) if path \(r\) is the optimal route for vehicle \(k\), and \(y^{k}_{r} = 0\) otherwise. Any solution to \(x^{k}_{ij}\) can now be expressed in terms of \(x^{k}_{ijr}\) and \(y^{k}_{r}\).

\[\sum_{r \in R^k} x^{k}_{ijr}y^{k}_{r} = x^{k}_{ij} \quad \forall k \in K, \forall (i,j) \in E \tag{11}\] \[\sum_{r \in P^k} y^{k}_{r} = 1 \quad \forall k \in K \tag{12}\] \[y^{k}_{r} = \{0,1\}\forall k \in K, \quad \forall r \in R^{k} \tag{13}\]

Using \(x^{k}_{ijr}\), we can also define the cost of a route, \(c^{k}_{r}\), and the number of times a customer is visited on that route, \(a^{k}_{ir}\) as below.

\[c^{k}_{r} = \sum_{(i,j) \in E} c^{k}_{ij}x^{k}_{ijr} \quad \forall k \in K,\ \forall r \in R^k \tag{14}\] \[a^{k}_{ir} = \sum_{\{j \in V \mid (i,j) \in E\}} x^{k}_{ij} \quad \forall k \in K,\ \forall i \in V,\ {\forall r \in R^k} \tag{15}\]

Now we can make use of \((11) - (15)\) to reformulate the master problem. Again, the master problem’s objective is to find the set of optimal routes that visit each customer exactly once and minimize total traveling cost. Substitute \((11) - (15)\) into equation \((1) - (2)\) and \((10)\) we obtain.

\[\text{Min} \quad \sum_{k \in K}\sum_{r \in R^k} c^{k}_{r}y^{k}_{r} \tag{16}\] \[\text{S.t.} \quad \sum_{k \in K}\sum_{r \in R^k} a^{k}_{ir}y^{k}_{r} = 1 \quad \forall i \in V{\setminus}\{0\} \tag{17}\] \[\sum_{r \in R^k} y^{k}_{r} = 1 \quad \forall k \in K \tag{18}\] \[y^{k}_{r} = \{0,1\} \quad \forall r \in R \tag{19}\]

Notice that all vehicles have identical capacity, initial conditions. Furthermore, the network structures for the subproblem of each vehicle are also identical. Therefore, the index \(k\) in the formulation above can be eliminated by letting \(R^{k} = R\), \(\forall k \in K\) and \(y_r = \sum_{k \in K} y^{k}_{r}\). The resulting master model is called a \textbf{set-partitioning model}.

\[\text{Min} \quad\sum_{r \in R} c_{r}y_{r} \tag{20}\] \[\text{S.t.} \quad \sum_{r \in R} a_{ir}y_{r} = 1 \quad \forall i \in V{\setminus}\{0\} \tag{21}\] \[y_{r} = \{0,1\} \quad \forall r \in R^k \tag{22}\]

A relaxed version of the set-partitioning model has some modifications. First, a route can visit a customer more than once, transforming the subprolem from the ESPPRC to the SPPRC. As a result, \(a_{ir}\) is transformed from binary variable type to integer variable type, which indicates the number of times a customer is visited on a route. In addition, binary decision variable \(y_r\) is relaxed to have any value in the continuous domain \([0,1]\). The reformulated master model is now a set-covering model.

\[\text{Min} \quad \sum_{r \in R} c_{r}y_{r} \tag{23}\] \[\text{S.t.} \quad \sum_{r \in R} a_{ir}y_{r} \geq 1 \quad \forall i \in V{\setminus}\{0\} \tag{24}\] \[0 \leq y_{r} \leq 1 \quad \forall r \in R^k \tag{25}\]

Subproblem

The subproblem, also called as pricing problem, is a NP-hard SPPRC. Two resources consumed along each path are time and capacity. The dual variables of the master problem, \(\pi_i\), are important to solve the subproblem. They enable the subproblem to generate routes with negative reduced costs. Such routes are then inserted to the master problem and solved for the next iteration.

To solve the master problem, apply simplex method to solve its set covering model. Let this model be the primal programming model. It can be easily seen that this model is in standard minimization form. Let \(\pi_{i}\), \(\forall i \in V\setminus\{0\}\) be the dual variables of the dual programming model. From primal-dual linear programming theory, the reduce cost \({\hat{c}}_{r}\) of each variable \(y_r\) can be easily defined as:

\[{\hat{c}}_{r} = c_{r} \quad – \sum_{i \in V \setminus \{0\}}\pi_{i}a_{ir} \tag{26}\]

The expression \((23)\) is equivalent to:

\[c_r = \sum_{(i,j)\in E}c_{ij}x_{ijr} \tag{27}\]

The reduced cost of an arc is then:

\[{\hat{c}}_{ij} = c_{ij} - \pi_{i} \tag{28}\]

The goal of the subproblem is to generate routes with negative reduced costs in order to improve the master problem solution.